オフポリシーモンテカルロ制御を用いた強化学習レーストラックの演習問題の解決

オフポリシーモンテカルロ制御を用いた強化学習レーストラックの演習問題の解決' can be condensed to 'オフポリシーモンテカルロ制御を用いたレーストラックの演習問題の解決

はじめに

『強化学習入門 第2版』（112ページ）の「オフポリシーモンテカルロ制御」のセクションでは、興味深い演習問題が用意されています。重み付きインポータンスサンプリングオフポリシーモンテカルロ法を使用して、両方のトラックで最も速く運転する方法を見つけるというものです。この演習は、環境、エージェント、報酬、アクション、終了条件、およびアルゴリズムなど、強化学習タスクのほぼすべてのコンポーネントを考慮して構築するよう求めています。この演習を解くことは楽しく、アルゴリズムと環境の相互作用、正しいエピソードタスクの定義の重要性、および値の初期化がトレーニングの結果にどのように影響するかについての確かな理解を築くのに役立ちます。この記事を通じて、強化学習に興味のあるすべての方と私の理解とこの演習の解決策を共有したいと思います。

演習の要件

前述のように、この演習では、レースカーがスタートラインからゴールラインまでできるだけ速く走行するポリシーを見つけるよう求められます。砂利やコース外に走り出さずに。演習の説明を注意深く読んだ後、このタスクを完了するために必要ないくつかのキーポイントをリストアップしました:

• マップの表現: この文脈では、マップは実際には2D行列であり、(行インデックス、列インデックス) が座標となります。各セルの値はそのセルの状態を表します。たとえば、砂利を示すために0を使用し、トラックの表面に1を使用し、スタート地点には0.4を、ゴールラインには0.8を使用することができます。行と列のインデックスが行列の範囲外の場合、境界外と見なすことができます。
• 車の表現: マトリックスの座標を直接車の位置を表すために使用することができます。
• 速度と制御: 速度空間は離散値であり、水平速度と垂直速度を含むタプル (行速度、列速度) として表すことができます。両軸の速度制限は (-5, 5) であり、各ステップで各軸に対して +1、0、および -1 ずつ増加します。したがって、各ステップで合計9つの可能なアクションがあります。速度は、スタートラインを除いてゼロになることはありませんし、垂直速度または行速度は負になることはありません。
• 報酬とエピソード: ゴールラインを越える前の各ステップの報酬は-1です。車がトラックから外れると、スタートセルのいずれかにリセットされます。エピソードは、車がゴールラインを成功裏に通過した場合にのみ終了します。
• スタート状態: スタートラインから車の開始セルをランダムに選択します。車の初期速度は、演習の説明に従って (0, 0) です。
• ゼロ加速度の課題: 著者は、各時間ステップで、0.1の確率でアクションが実行されず、車が前の速度でとどまるという小さなゼロ加速度の課題を提案しています。環境に機能を追加する代わりに、トレーニング中にこの課題を実装することができます。

この演習の解決策は2つの記事に分けています。この記事では、レーストラックの環境の構築に焦点を当てます。この演習のファイル構造は次のようになります:

|-- race_track_env|  |-- maps|  |  |-- build_tracks.py // このファイルはトラックマップを生成するために使用されます|  |  |-- track_a.npy // トラックAのデータ|  |  |-- track_b.npy // トラックBのデータ|  |-- race_track.py // レーストラック環境|-- exercise_5_12_racetrack.py // この演習の解決策

この実装で使用されるライブラリは次のとおりです:

• 完全に自動化されたデータドリフト検出パイプラインの構築方法
• 「高度なデータサイエンス技術を用いたEコマース詐欺の検出」
• データサイエンティストやアナリストのための統計の基礎

python==3.9.16numpy==1.24.3matplotlib==3.7.1pygame==2.5.0

トラックマップの構築

トラックマップを異なる値で示す2D行列として表現することができます。私はこの演習に忠実でありたいので、マトリックスの値を手動で割り当てることで、本に示されていると同じマップを作成しようとしています。マップは別々の .npy ファイルとして保存されるため、環境は実行時ではなくトレーニング中にファイルを読み込むことができます。

2つのマップは以下のようになります。明るいセルは砂利で、暗いセルはトラックの表面、緑色のセルはゴールラインを、薄い青色のセルはスタートラインを表しています。

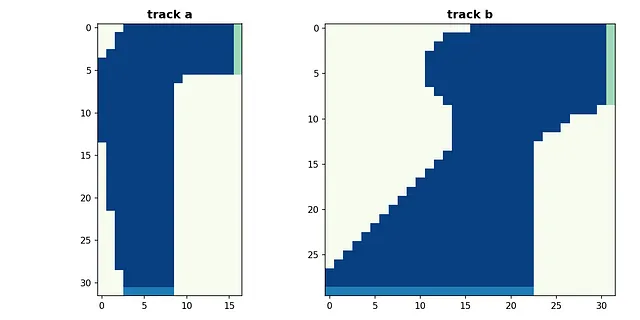
Gymのような環境の構築

トラックマップが準備できたので、アルゴリズムが相互作用できるGymのような環境を作成します。以前はOpenAI gymとして知られていたジムナジウムは、RLアルゴリズムのテストに使用するためのシンプルなインターフェースを提供します。ジムナジウムパッケージを使用してレーストラック環境を作成します。環境には以下のコンポーネント/機能が含まれます：

• env.nS: 観測空間の形状です。この例では(num_rows, num_cols, row_speed, col_speed)です。行数と列数はマップごとに異なりますが、速度空間はトラックごとに一貫しています。行速度はスタートラインに戻ることを避けたいため、行速度の観測は[-4、-3、-2、-1、0]（マップ内で車が上方向に進むことを期待しているため、負の値）の5スペースから構成されます。列速度にはこのような制限はありませんので、観測範囲は-4から4までの9スペースです。したがって、レーストラックの例では、観測空間の形状は(num_rows, num_cols, 5, 9)です。
• env.nA: 可能なアクションの数です。この実装では9つのアクションが可能です。また、環境クラス内に整数アクションを（row_speed、col_speed）のタプル表現にマップするための辞書も作成します。
• env.reset(): エピソードが終了した場合や車がトラックから外れた場合に、車をスタートセルの1つに戻す関数です。
• env.step(action): ステップ関数は、アクションを実行し、（next_state、reward、is_terminated、is_truncated）のタプルを返すことでアルゴリズムが環境と相互作用できるようにします。
• 状態チェック関数：車がトラックを離れたかゴールラインを越えたかをチェックするための2つのプライベート関数があります。
• レンダリング関数：カスタマイズされた環境には、レンダリング関数が不可欠です。ゲームスペースとエージェントの振る舞いをレンダリングして、環境が正しく構築されたかどうかを確認します。これは、ログ情報をただ眺めるよりも簡単です。

これらの機能を考慮しながら、レーストラック環境の構築を開始できます。

環境の確認

これまでに、レーストラック環境に必要なすべての準備が整ったので、環境のセットアップをテスト/検証できます。

まず、ゲームプレイをレンダリングして、すべてのコンポーネントが正常に動作しているかを確認します：

図2 ランダムポリシーで両方のトラックを走行するエージェント。出典: 著者によるGif

次に、レンダーオプションをオフにして、軌跡が正しく終了するかを確認するために環境をバックグラウンドで実行します：

// Track a|   観測   | 報酬 | 終了 | 累積報酬 ||  (1, 16, 0, 3)  |   -1   |  True  |  -4984   ||  (2, 16, 0, 2)  |   -1   |  True  |  -23376  ||  (3, 16, 0, 3)  |   -1   |  True  |  -14101  ||  (1, 16, 0, 3)  |   -1   |  True  |  -46467  |// Track b|   観測    | 報酬 | 終了 | 累積報酬 ||  (1, 31, -2, 2)  |   -1   |  True  |  -3567   ||  (0, 31, -4, 4)  |   -1   |  True  |  -682    ||  (2, 31, -2, 1)  |   -1   |  True  |  -1387   ||  (3, 31, -1, 3)  |   -1   |  True  |  -2336   |

オフポリシー・モンテカルロ制御アルゴリズム

環境の準備が整ったら、以下に示す重み付き重要度サンプリングアルゴリズムを使ってオフポリシー・モンテカルロ制御アルゴリズムを実装する準備ができます。

モンテカルロ法は、サンプルリターンの平均化によって強化学習問題を解決します。トレーニングでは、この方法は与えられたポリシーに基づいて軌跡を生成し、各エピソードの末尾から学習します。オンポリシーとオフポリシーの違いは、オンポリシーメソッドは1つのポリシーを使用して意思決定と改善を行うのに対し、オフポリシーメソッドはデータの生成とポリシーの改善に別々のポリシーを使用することです。書籍の著者によると、ほとんどのオフポリシーメソッドは、別の分布からのサンプルを使用して1つの分布の下で期待値を推定するために重要度サンプリングを利用しています。[2]

以下の数節では、上記のアルゴリズムに現れるソフトポリシーと重み付き重要度サンプリングのトリック、および適切な値の初期化がこのタスクにどれだけ重要かについて説明します。

ターゲットポリシーとビヘイビアポリシー

このアルゴリズムのオフポリシーメソッドは2つのポリシーを使用します:

• ターゲットポリシー: 学習対象のポリシー。このアルゴリズムでは、ターゲットポリシーは貪欲かつ決定論的であり、時刻tでの貪欲なアクションAの確率は1.0であり、他のすべてのアクションの確率は0.0です。ターゲットポリシーは一般化ポリシー反復法（GPI）に従って改善されます。
• ビヘイビアポリシー: 行動の生成に使用されるポリシー。このアルゴリズムでは、ビヘイビアポリシーはソフトポリシーと定義されており、ある状態でのすべてのアクションが非ゼロの確率を持ちます。ここではε-グリーディポリシーをビヘイビアポリシーとして使用します。

ソフトポリシーでは、アクションの確率は次のようになります:

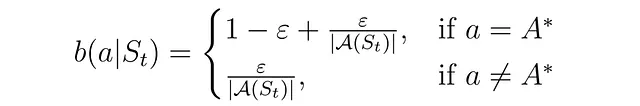
重要度サンプリングのためにアクションを生成する際にも、この確率を返す必要があります。ビヘイビアポリシーのコードは以下のようになります:

重み付き重要度サンプリング

ターゲットポリシーによって生成された軌跡のビヘイビアポリシーに対する相対確率を推定し、その確率の方程式は次のようになります:

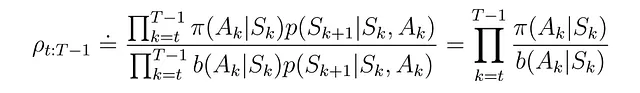
重み付き重要度サンプリングの値関数は次のようになります:

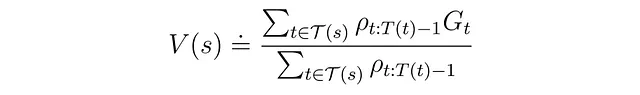
この方程式をエピソードタスクに合わせてインクリメンタルな更新の形に変換することができます:

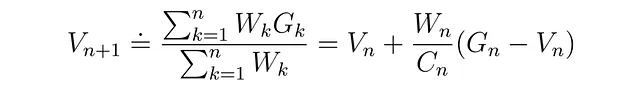
上記の方程式の導出については、すでに多くの優れた例が存在するため、ここでは導出に時間を費やしません。ただし、アルゴリズムの最後の数行についての興味深いトリックについて説明したいと思います:

このトリックは、ここでのターゲットポリシーが決定論的であるという設定に基づいています。時間ステップでのアクションがターゲットポリシーからのものと異なる場合、そのアクションのターゲットポリシーに対する確率は0.0になります。したがって、以降のすべてのステップは、軌跡の状態アクション価値関数の更新を行いません。逆に、その時間ステップでのアクションがターゲットポリシーと同じである場合、確率は1.0であり、アクション価値の更新が継続されます。

重みの初期化

適切な重みの初期化は、この演習を成功裏に解決する上で重要な役割を果たします。まずはランダムポリシーでの両トラックの報酬を見てみましょう：

// トラックa|   観測   | 報酬 | 終了 | 累計報酬 ||  (1, 16, 0, 3)  |   -1   |  True  |   -4984   ||  (2, 16, 0, 2)  |   -1   |  True  |  -23376   ||  (3, 16, 0, 3)  |   -1   |  True  |  -14101   ||  (1, 16, 0, 3)  |   -1   |  True  |  -46467   |// トラックb|   観測    | 報酬 | 終了 | 累計報酬 ||  (1, 31, -2, 2)  |   -1   |  True  |   -3567   ||  (0, 31, -4, 4)  |   -1   |  True  |   -682    ||  (2, 31, -2, 1)  |   -1   |  True  |  -1387    ||  (3, 31, -1, 3)  |   -1   |  True  |  -2336    |

ゴールラインを越えるまでの各タイムステップでの報酬は-1です。トレーニングの初期段階では、報酬は負の大きな値になります。状態-行動価値を0または正規分布（平均0、分散1）のランダムな値で初期化すると、値は非常に楽観的すぎて、最適なポリシーを見つけるのに非常に長い時間がかかる可能性があります。

いくつかのテストの結果、平均が-500で分散が1の正規分布は、収束が速くなる効果的な値であることがわかりました。他の値を試して、これよりも優れた初期値を見つけることができます。

問題の解決

上記のすべての考えを念頭に置いて、オフポリシーモンテカルロ制御関数をプログラム化し、レーストラックの演習を解くために使用することができます。また、演習の説明で言及されているゼロアクセラレーションの課題も追加します。

次に、両トラックでゼロアクセラレーションのチャレンジの有無に関係なく、1,000,000エピソードのポリシーをトレーニングし、次のコードで評価します：

トレーニングの記録をプロットすることで、ポリシーがゼロアクセラレーションを考慮しない場合には10,000エピソード前後で収束することがわかります。ゼロアクセラレーションを追加すると、収束は100,000エピソード前には遅くなり不安定になりますが、その後も収束します。

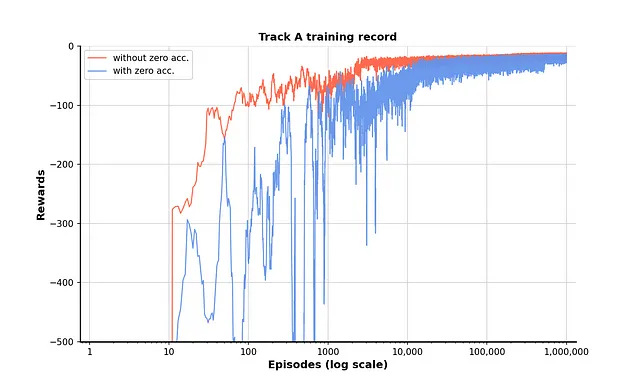
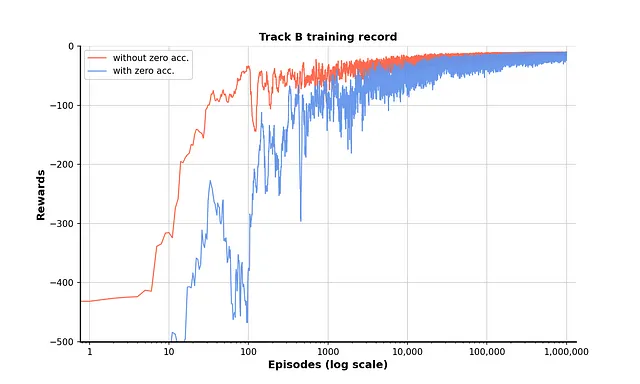
結果

最後に、エージェントにトレーニングされたポリシーでゲームをプレイしてもらい、ポリシーの正確性をさらにチェックするために可能な軌跡をプロットします。

図7 トレーニングされたポリシーに基づいて両トラック上を走行するエージェント。出典：著者によるGif

トラックaのサンプル軌跡：

トラックbのサンプル軌跡：

これまでに、私たちはレーストラックのエクササイズを解決しました。この実装にはまだいくつかの問題があるかもしれませんので、コメントで指摘して改善策を議論することは大歓迎です。読んでいただきありがとうございます！

参考文献

[1] Midjourney利用規約：https://docs.midjourney.com/docs/terms-of-service

[2] Sutton, Richard S.、およびAndrew G. Barto。強化学習：入門。MIT Press、2018年。

このエクササイズの私のGitHubリポジトリ：[リンク]。”exercise section”をご確認ください。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!