アップリフトモデルの評価

アップリフトモデル評価

因果データサイエンス

最適なアップリフトモデルを比較・選択する方法

業界における因果推論の最も広く普及している応用の1つは、アップリフトモデリング、または条件付き平均処置効果の推定です。

「処置」（薬物、広告、製品など）の「結果」（疾患、企業収益、顧客満足度など）に対する因果効果を推定する際に、私たちは通常、処置が平均的に機能するかどうかだけでなく、どの「対象者」（患者、ユーザー、顧客など）に対してより良くまたは悪く機能するかを知りたいと思っています。

異質な増分効果、またはアップリフトの推定は、対象政策の「ターゲティング」を改善するための重要な中間ステップです。例えば、特定の人々に、薬物の副作用がより起こりやすいことを警告したり、特定の顧客セットに広告を表示したりしたい場合があります。

アップリフトをモデル化するための多くの方法が存在しますが、特定のアプリケーションでどれを使用するかは常に明確ではありません。因果推論の基本的な問題のために、興味の対象であるアップリフトは観測されないため、機械学習の予測アルゴリズムと同様に推定器を検証することはできません。確かな「正解」はなく、検証セットにも含まれておらず、ランダム化試験を実施しても得られません。

• 「知識グラフの力を利用する：構造化データでLLMを豊かにする」
• 「Pythonデータ構造について知っておくべき3つの重要な概念」
• 「Jaro-Winklerアルゴリズムを使用して小規模言語モデル（SLM）を構築し、スペルエラーを改善・強化する」

では、どうすればよいのでしょうか？この記事では、アップリフトモデルを評価するために最も一般的な方法について説明します。アップリフトモデルについて詳しく知りたい場合は、まず私の入門記事を読むことをお勧めします。

メタラーナーの理解

説明の編集

towardsdatascience.com

アップリフトとプロモーションメール

私たちが所属している製品会社のマーケティング部門で、メールマーケティングキャンペーンを改善したいと思っています。過去には主に新規顧客にメールを送信していました。しかし、今ではデータに基づいたアプローチを取り入れ、収益に最もポジティブな影響を与える顧客をターゲットにしたいと考えています。この影響をアップリフトまたは増分効果とも呼びます。

利用可能なデータを見てみましょう。私はsrc.dgpからdgp_promotional_email()というデータ生成プロセスをインポートします。また、src.utilsからいくつかのプロット関数とライブラリをインポートします。

from src.utils import *from src.dgp import dgp_promotional_emaildgp = dgp_promotional_email(n=500)df = dgp.generate_data()df.head()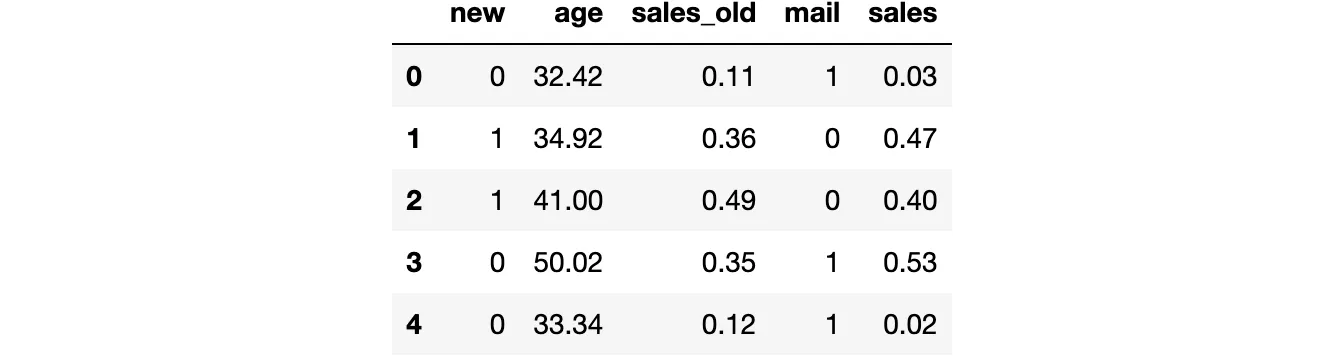

私たちは500人の顧客の情報を持っており、new顧客かどうか、age、メールキャンペーン前に生成された売上（sales_old）、メールを送信したかどうか（mail）、およびメールキャンペーン後の売上（sales）を観察します。

興味のある結果はsalesであり、これをYと表記します。改善したい処置または方針は、メールキャンペーンであり、これをWと表記します。残りの変数を共変量または制御変数と呼び、Xで表記します。

Y = 'sales'W = 'mail'X = ['age', 'sales_old', 'new']

変数間の因果関係を表す有向非巡回グラフ（DAG）は次のとおりです。興味のある因果関係は緑色で描かれています。

DAGから、new顧客指標は混入因子であり、salesに対するmailの影響を特定するために制御する必要があります。一方、ageとsales_oldは推定には必要ありませんが、識別に役立つ可能性があります。DAGと制御変数に関する詳細情報については、私の入門記事をご覧ください。

DAGと制御変数

説明を編集する

towardsdatascience.com

アップリフトモデリングの目的は、プロモーションのmailを送信することによるsalesへの個別処置効果（ITE） τᵢを推定することです。ITEは、顧客がメールを受け取った場合のポテンシャルアウトカム Yᵢ⁽¹⁾ と、顧客がメールを受け取らなかった場合のポテンシャルアウトカム Yᵢ⁽⁰⁾ の差として表現することができます。

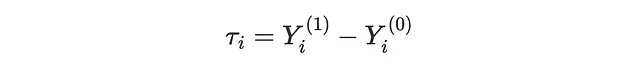
各顧客について、実際にmailを受け取ったかどうかに応じて、2つの実現されたアウトカムのうちの1つしか観察されません。したがって、ITEは本質的に観測不可能です。代わりに推定できるのは、共変量Xに条件付けられた期待個別処置効果（CATE）であり、つまり、年齢が50歳以上の顧客に対するmailのsalesに対する平均効果です。

CATEを復元するためには、3つの仮定をする必要があります。

1. 無相関性: Y⁽⁰⁾, Y⁽¹⁾ ⊥ W | X
2. 重複: 0 < e(X) < 1
3. 一貫性: Y = W ⋅ Y⁽¹⁾ + (1−W) ⋅ Y⁽⁰⁾

ここで、e(X)は共変量Xに条件付けられた処置を受ける確率である傾向スコアです。

次に、機械学習手法を使用して、CATE τ(x)、傾向スコア e(x)、およびアウトカムの条件付き期待関数（CEF）μ(x)を推定します。

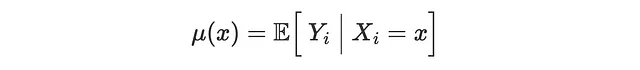
私たちは、CATEとアウトカムCEFをモデル化するためにランダムフォレスト回帰アルゴリズムを使用し、傾向スコアをモデル化するためにロジスティック回帰を使用しています。

from sklearn.ensemble import RandomForestRegressorfrom sklearn.linear_model import LogisticRegressionCVmodel_tau = RandomForestRegressor(max_depth=2)model_y = RandomForestRegressor(max_depth=2)model_e = LogisticRegressionCV()

この記事では、基礎となる機械学習モデルを微調整していませんが、アップリフトモデルの精度を向上させるためには微調整が強く推奨されています（たとえば、FLAMLのような自動機械学習ライブラリを使用して）。

アップリフトモデル

アップリフトまたは条件付き平均処置効果（CATE）を推定するための多くの方法が存在します。この記事の目的は、アップリフトモデルを評価する方法を比較することであるため、方法については詳しく説明しません。入門記事として、メタラーナーに関する私の紹介記事を参照してください。

考慮する学習モデルは以下の通りです：

• S-learnerまたはシングルラーナー（Kunzel、Sekhon、Bickel、Yu、2017年に導入）
• T-learnerまたはツーラーナー（Kunzel、Sekhon、Bickel、Yu、2017年に導入）
• X-learnerまたはクロスラーナー（Kunzel、Sekhon、Bickel、Yu、2017年に導入）
• R-learnerまたはロビンソンラーナー（Nie、Wager、2017年に導入）
• DR-learnerまたはダブルロバストラーナー（Kennedy、2022年に導入）

Microsoftのeconmlライブラリからすべてのモデルをインポートします。

from src.learners_utils import *from econml.metalearners import SLearner, TLearner, XLearnerfrom econml.dml import NonParamDMLfrom econml.dr import DRLearnerS_learner = SLearner(overall_model=model_y)T_learner = TLearner(models=clone(model_y))X_learner = XLearner(models=model_y, propensity_model=model_e, cate_models=model_tau)R_learner = NonParamDML(model_y=model_y, model_t=model_e, model_final=model_tau, discrete_treatment=True)DR_learner = DRLearner(model_regression=model_y, model_propensity=model_e, model_final=model_tau)

データ上でモデルをfit()します。アウトカム変数Y、処置変数W、および共変量Xを指定します。

names = ['SL', 'TL', 'XL', 'RL', 'DRL']learners = [S_learner, T_learner, X_learner, R_learner, DR_learner]for learner in learners:    learner.fit(df[Y], df[W], X=df[X])

モデルの評価に備えて準備が整いました！どのモデルを選ぶべきでしょうか？

オラクル損失関数

アップリフトモデルの評価の主な問題は、検証セットやランダム化実験またはABテストを行っても、興味のある指標である個別処置効果を観測できないことです。実際には、処理されていない顧客の実現アウトカムYᵢ⁽⁰⁾および処理された顧客の実現アウトカムYᵢ⁽¹⁾のみを観測します。したがって、任意の顧客に対して検証データで個別処置効果τᵢ = Yᵢ⁽¹⁾ − Yᵢ⁽⁰⁾を計算することはできません。

それでもエスティメーターを評価するために何かできることはありますか？

答えは「はい」ですが、詳細を説明する前に、もし個別処置効果τᵢを観測できる場合に何をするかを理解しましょう。

オラクルMSE損失

個別処置効果を観測できる場合（しかし実際にはできないため、「オラクル」属性が付いています）、推定値τ̂(Xᵢ)が真の値τᵢからどれだけ離れているかを測定しようとします。これは、予測手法を評価するための通常の機械学習で行うことです。検証データセットを確保し、そのデータ上で予測値と真の値を比較します。予測精度を評価するための損失関数はたくさんありますが、最も一般的なものである平均二乗誤差（MSE）損失に焦点を当てましょう。

def loss_oracle_mse(data, learner):    tau = learner.effect(data[X])    return np.mean((tau - data['effect_on_sales'])**2)

関数compare_methodsは、別の検証データセットで計算された評価メトリックスを表示およびプロットします。

def compare_methods(learners, names, loss, title=None, subtitle='下が良い'):    data = dgp.generate_data(seed_data=1, seed_assignment=1, keep_po=True)    results = pd.DataFrame({        'learner': names,        'loss': [loss(data.copy(), learner) for learner in learners]    })    fig, ax = plt.subplots(1, 1, figsize=(6, 4))    sns.barplot(data=results, x="learner", y='loss').set(ylabel='')    plt.suptitle(title, y=1.02)    plt.title(subtitle, fontsize=12, fontweight=None, y=0.94)    return resultsresults = compare_methods(learners, names, loss_oracle_mse, title='オラクルMSE損失')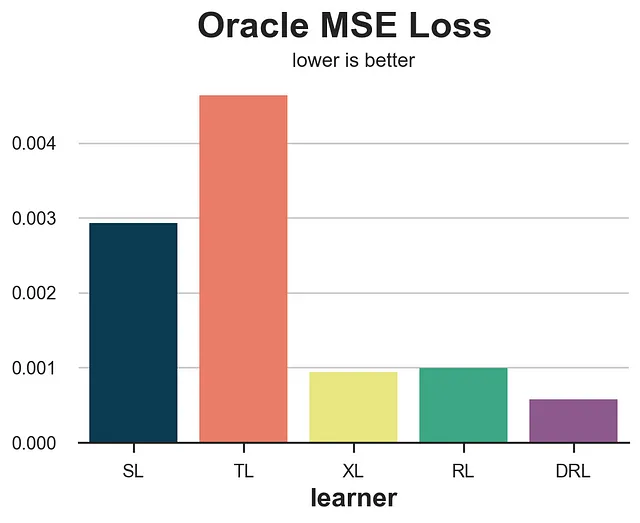

この場合、T-learnerが明らかに最も悪く、S-learnerがその直後に続きます。一方、X-、R-、およびDR-learnersははるかに優れたパフォーマンスを発揮し、DR-learnerが競争を制しています。

ただし、これは私たちのアップリフトモデルを評価するための最良の損失関数ではないかもしれません。実際には、アップリフトモデリングは究極の目標である収益向上への中間ステップに過ぎません。

オラクルポリシーゲイン

私たちの究極の目標は収益の向上ですので、ある特定のポリシー関数を与えられた場合に、推定器がどれだけ収益を増加させるかを評価することができます。例えば、メール送信のコストが0.01ドルだとすると、各顧客に対して予測された平均条件付き処置効果が0.01ドル以上であると判断するポリシーを採用します。

cost = 0.01

実際に収益はどれだけ増加するでしょうか？d(τ̂)を私たちのポリシー関数と定義しましょう。τ ≥ 0.1の場合、d=1とし、それ以外の場合はd=0とします。すると、私たちのゲイン（高い方が良い）関数は次のようになります：

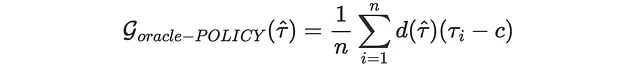
また、これは実際には計算できない「オラクル」の損失関数であり、個々の処置効果を観察することができないため、現実では計算できません。

def gain_oracle_policy(data, learner):    tau_hat = learner.effect(data[X])    return np.sum((data['effect_on_sales'] - cost) * (tau_hat > cost))results = compare_methods(learners, names, gain_oracle_policy, title='オラクルポリシーゲイン', subtitle='高い方が良い')

この場合、S-learnerは明らかに最もパフォーマンスが悪く、収益に影響を与えません。T-learnerはわずかな利益をもたらし、X-、R-、およびDR- learnersはすべて集計の利益をもたらし、X-learnerがわずかに優位です。

実用的な損失関数

前のセクションでは、個々の処置効果τᵢを観測できる場合に計算したい2つの損失関数の例を見てきました。しかし、実際には、ランダム化実験を行っても、検証セットを持っていても、私たちは興味の対象であるITEを観測することはありません。このような制約のもとで、アップリフトモデルを評価するためにいくつかの指標をカバーします。

アウトカムの損失

最初で最もシンプルなアプローチは、異なる損失変数に切り替えることです。個別の処置効果τᵢは観測できませんが、アウトカムYᵢは観測できます。これは正確には私たちの興味の対象ではありませんが、yを予測するうえで優れた性能を発揮するアップリフトモデルは、τの良い推定値も生成する可能性があります。

このような損失関数の一つは、アウトカムMSE損失であり、予測方法の通常のMSE損失関数です。

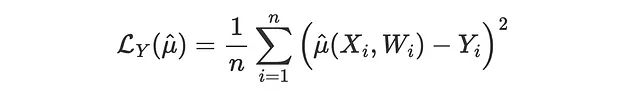
問題は、すべてのモデルがμ(x)の推定値を直接生成しないということです。したがって、この比較をスキップし、アップリフトモデルを評価できる方法に切り替えます。

予測から予測への損失

もう一つ非常にシンプルなアプローチは、トレーニングセットで訓練されたモデルの予測と、バリデーションセットで訓練された別のモデルの予測を比較することです。直感的ではありますが、このアプローチは非常に誤解を招く可能性があります。

def loss_pred(data, learner):    tau = learner.effect(data[X])    learner2 = copy.deepcopy(learner).fit(data[Y], data[W], X=data[X])    tau2 = learner2.effect(data[X])    return np.mean((tau - tau2)**2)results = compare_methods(learners, names, loss_pred, '予測から予測への損失')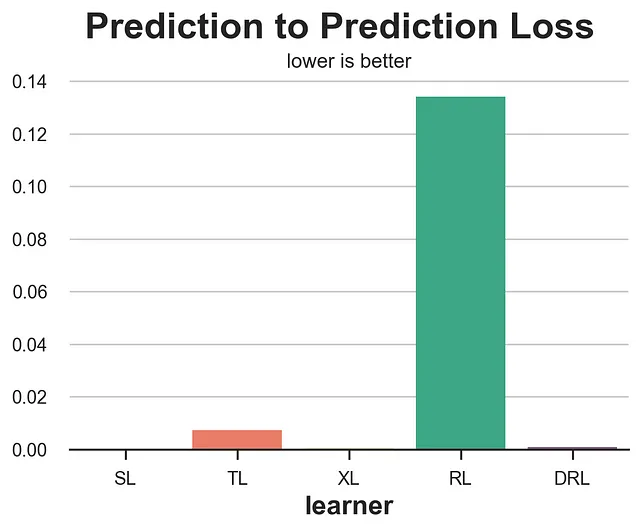

予想通り、この指標は非常に悪いパフォーマンスを示し、品質に関係なく一貫性のあるモデルを報酬としてしまうため、使用しないでください。各観測に対してランダムな定数CATEを常に予測するモデルは完璧なスコアを獲得します。

分布の損失

別のアプローチは次のような質問をすることです：潜在的なアウトカムの分布をどれだけマッチングできるでしょうか？処置を受けた場合または処置を受けなかった場合の潜在的なアウトカムのどちらに対してもこの演習を行うことができます。ここでは、最後のケースを取り上げます。受け取ったmailを受けなかった顧客の観測されたsalesと、mailを受け取った顧客の観測されたsalesから推定されたCATE τ̂(x)を引いたものを考えます。非交絡性の仮定により、これらの2つの未処置の潜在的なアウトカムの分布は、共変量Xに条件付けられた場合に類似しているはずです。

したがって、私たちは、処置効果を正しく推定できている場合、2つの分布間の距離が近いことを期待しています。

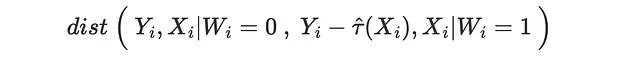
同じ演習を処置された潜在的なアウトカムに対しても行うことができます。

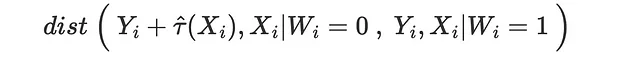
距離尺度としてエネルギー距離を使用しています。

from dcor import energy_distancedef loss_dist(data, learner):    tau = learner.effect(data[X])    data.loc[data.mail==1, 'sales'] -= tau[data.mail==1]    return energy_distance(data.loc[data.mail==0, [Y] + X], data.loc[data.mail==1, [Y] + X], exponent=2)results = compare_methods(learners, names, loss_dist, '分布の損失')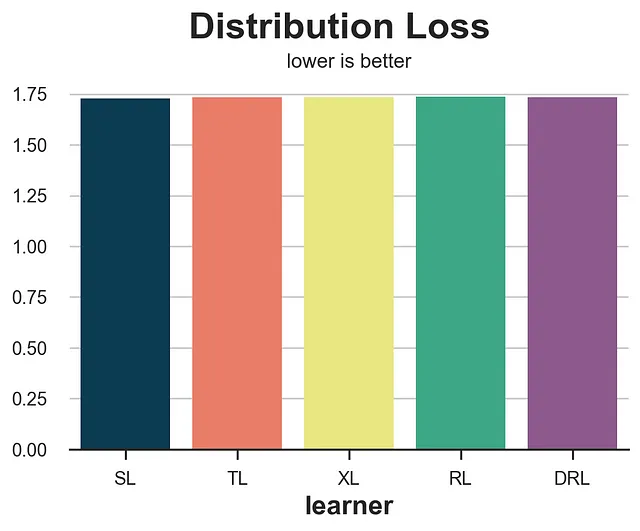

この指標は非常にノイズが多く、実際には最もパフォーマンスの悪いモデルであるS-learnerとT-learnerを報酬としています。

上下中央値の差

上下中央値の損失は、次の問いに答えようとします：私たちのアップリフトモデルはいかなる異質性を検出しているのか？特に、検証セットを取り、サンプルを中央値以上と中央値以下の予測されたアップリフトτ̂(x)に分割した場合、平均効果の実際の差はどれくらい大きいでしょうか？良い推定器は、サンプルを高効果と低効果によりよく分割することが期待されます。

from statsmodels.formula.api import ols def loss_ab(data, learner):    tau = learner.effect(data[X]) + np.random.normal(0, 1e-8, len(data))    data['above_median'] = tau >= np.median(tau)    param = ols('sales ~ mail * above_median', data=data).fit().params[-1]    return paramresults = compare_methods(learners, names, loss_ab, title='上下中央値の差', subtitle='より高いほど良い')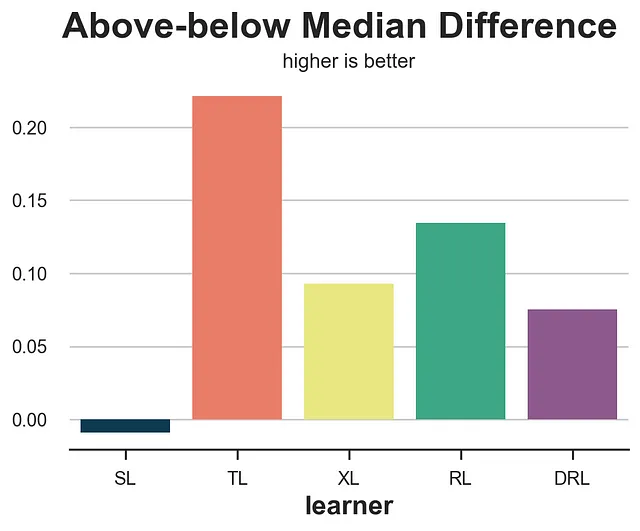

残念ながら、上下中央値の差は最もパフォーマンスの悪いモデルであるT-learnerを報酬としています。

データがランダム化実験から得られたとしても、上下中央値の差の両群（上位と下位の中央値τ̂(x)）の平均値の差は、バイアスがないとは限りません。実際には、非常に内生的な変数τ̂(x)で2つのグループを分割しています。そのため、この手法は慎重に使用する必要があります。

アップリフト曲線

上下中央値テストの拡張として、アップリフト曲線があります。アイデアはシンプルです：中央値（0.5の分位数）に基づいてサンプルを2つのグループに分割する代わりに、より多くのグループ（より多くの分位数）にデータを分割することはできませんか？

各グループについて、平均値の差の推定値を計算し、対応する分位点に対して累積和をプロットします。その結果がアップリフト曲線です。解釈は簡単です：曲線が高いほど、高効果と低効果の観測値をより良く分離できます。ただし、同じ警告が適用されます：平均値の差の推定値はバイアスがありません。そのため、慎重に使用する必要があります。

def generate_uplift_curve(df):    Q = 20    df_q = pd.DataFrame()    data = dgp.generate_data(seed_data=1, seed_assignment=1, keep_po=True)    ate = np.mean(data[Y][data[W]==1]) - np.mean(data[Y][data[W]==0])    for learner, name in zip(learners, names):        data['tau_hat'] = learner.effect(data[X])        data['q'] = pd.qcut(-data.tau_hat + np.random.normal(0, 1e-8, len(data)), q=Q, labels=False)        for q in range(Q):            temp = data[data.q <= q]            uplift = (np.mean(temp[Y][temp[W]==1]) - np.mean(temp[Y][temp[W]==0])) * q / (Q-1)            df_q = pd.concat([df_q, pd.DataFrame({'q': [q], 'uplift': [uplift], 'learner': [name]})], ignore_index=True)        fig, ax = plt.subplots(1, 1, figsize=(8, 5))    sns.lineplot(x=range(Q), y=ate*range(Q)/(Q-1), color='k', ls='--', lw=3)    sns.lineplot(x='q', y='uplift', hue='learner', data=df_q);    plt.suptitle('アップリフト曲線', y=1.02, fontsize=28, fontweight='bold')    plt.title('より高いほど良い', fontsize=14, fontweight=None, y=0.96)generate_uplift_curve(df)

アップリフトモデルを評価するための最良の方法ではないかもしれませんが、アップリフト曲線は非常に重要です。実際、各モデルについて、処置を受けた人口の割合（x軸）を増やすと、期待される平均処置効果（y軸）を教えてくれます。

最近傍マッチング

前回のいくつかの方法では、大きなグループでの動作を確認するために集計されたデータを使用しました。最近傍マッチングでは、アップリフトモデルが個々の処置効果をどれだけよく予測するかを理解しようとします。しかし、処置効果は観測できないため、可視化される特徴量Xに基づいて処置群と対照群の観測値をマッチングして、代理変数を構築しようとします。

たとえば、処置を受けた全ての観測値（i: Wᵢ=1）を取り、対照群で最も近い近傍値（NN₀(Xᵢ)）を見つけた場合、対応するMSE損失関数は次のようになります。

from scipy.spatial import KDTreedef loss_nn(data, learner):    tau_hat = learner.effect(data[X])    nn0 = KDTree(data.loc[data[W]==0, X].values)    control_index = nn0.query(data.loc[data[W]==1, X], k=1)[-1]    tau_nn = data.loc[data[W]==1, Y].values - data.iloc[control_index, :][Y].values    return np.mean((tau_hat[data[W]==1] - tau_nn)**2)results = compare_methods(learners, names, loss_nn, title='最近傍損失')

この場合、最近傍損失は非常に良い結果を示し、S-およびT-learnerという2つの最も悪いパフォーマンスを示す方法を特定します。

IPW損失

逆確率重み付け（IPW）損失関数は、Gutierrez, Gerardy（2017）によって最初に提案されたもので、推定量を評価するために擬似アウトカムY*を使用する3つのメトリックの最初のものです。擬似アウトカムは、条件付き平均処置効果の期待値でありながら、直接的な推定値として使用するには不安定すぎる変数です。擬似アウトカムに対応するIPW損失は次のようになります。

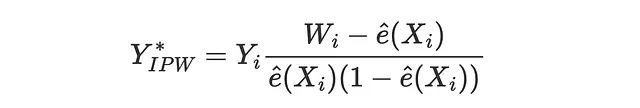
そのため、対応する損失関数は次のようになります。

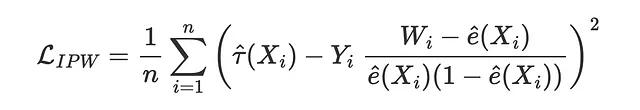
def loss_ipw(data, learner):    tau_hat = learner.effect(data[X])    e_hat = clone(model_e).fit(data[X], data[W]).predict_proba(data[X])[:,1]    tau_gg = data[Y] * (data[W] - e_hat) / (e_hat * (1 - e_hat))    return np.mean((tau_hat - tau_gg)**2)results = compare_methods(learners, names, loss_ipw, title='IPW損失')

IPW損失は非常にノイズが多いです。解決策として、より頑健なバリエーションであるR-lossまたはDR-lossを使用することがあります。

R Loss

R-lossは、Nie、Wager（2017）によってR-learnerと共に導入され、実質的にはR-learnerの目的関数です。IPW-lossと同様に、アイデアは条件付き平均治療効果の期待値と一致する疑似アウトカムをマッチングしようとすることです。

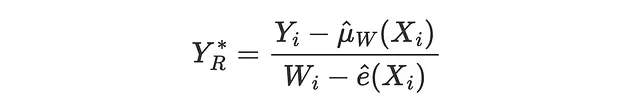
対応する損失関数は次のようになります。

def loss_r(data, learner):    tau_hat = learner.effect(data[X])    y_hat = clone(model_y).fit(df[X + [W]], df[Y]).predict(data[X + [W]])    e_hat = clone(model_e).fit(df[X], df[W]).predict_proba(data[X])[:,1]    tau_nw = (data[Y] - y_hat) / (data[W] - e_hat)    return np.mean((tau_hat - tau_nw)**2)compare_methods(learners, names, loss_r, title='R Loss')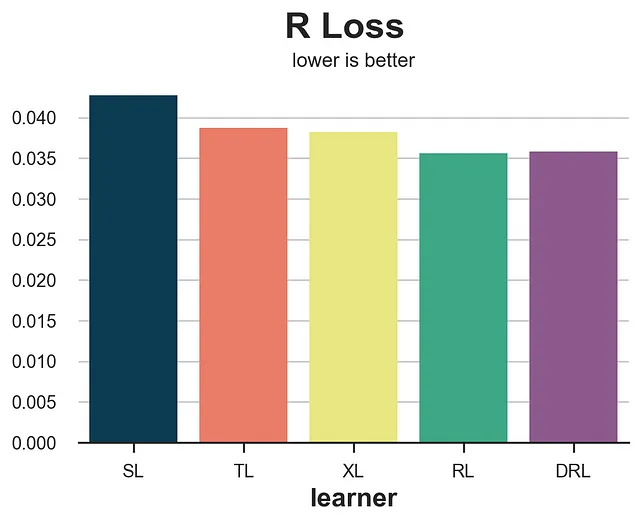

R損失はIPW損失よりもノイズが少なく、S-learnerを明確に分離します。ただし、対応する学習器であるR-learnerを好む傾向があります。

DR Loss

DR-lossはDR-learnerの目的関数であり、Saito、Yasui（2020）によって最初に導入されました。IPWおよびR-lossと同様に、アイデアは条件付き平均治療効果の期待値と一致する疑似アウトカムをマッチングしようとすることです。DR疑似アウトカムは、AIPW推定量（二重ロバスト推定量とも呼ばれる）に強く関連しています。

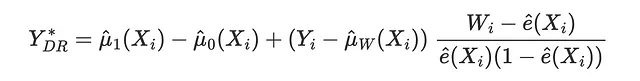
対応する損失関数は次のようになります。

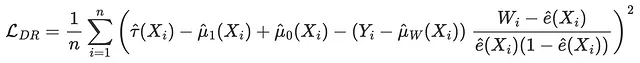
def loss_dr(data, learner):    tau_hat = learner.effect(data[X])    y_hat = clone(model_y).fit(df[X + [W]], df[Y]).predict(data[X + [W]])    mu1 = clone(model_y).fit(df[X + [W]], df[Y]).predict(data[X + [W]].assign(mail=1))    mu0 = clone(model_y).fit(df[X + [W]], df[Y]).predict(data[X + [W]].assign(mail=0))    e_hat = clone(model_e).fit(df[X], df[W]).predict_proba(data[X])[:,1]    tau_nw = mu1 - mu0 + (data[Y] - y_hat) * (data[W] - e_hat) / (e_hat * (1 - e_hat))    return np.mean((tau_hat - tau_nw)**2)results = compare_methods(learners, names, loss_dr, title='DR Loss')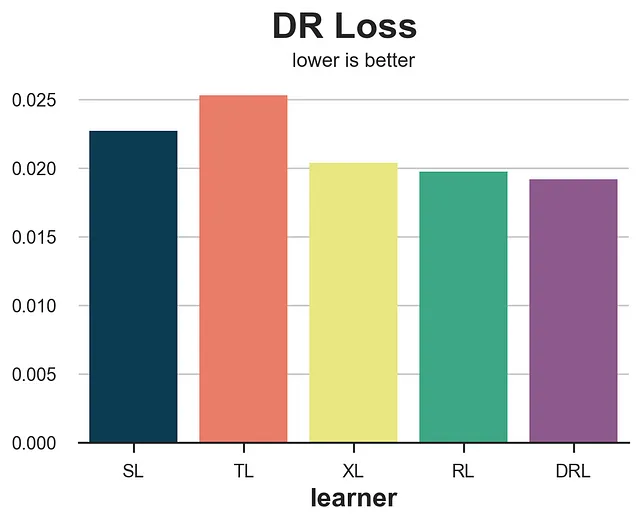

Rロスに関して、DRロスはそれに対応する学習モデルであるDR-learnerを好む傾向があります。ただし、アルゴリズムの精度に基づいたより正確なランキングを提供します。

経験的方策利得

これまで見てきた他のすべての損失関数とは異なり、経験的方策利得は治療効果をどれだけ正確に推定できるかではなく、対応する最適治療方針がどれほど良いパフォーマンスを発揮するかに焦点を当てています。具体的には、Hitsch、Misra、Zhang（2023）は次の利得関数を提案しています。

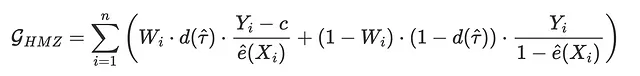
ここで、cは治療のコストであり、dは推定されたCATE τ̂(Xᵢ)に基づく最適治療方針です。この場合、個別の治療費用c=0.01$を前提とし、推定されたCATEが0.01より大きい顧客には治療を行うことが最適方針となります。

Wᵢ⋅d(τ̂)と(1-Wᵢ)⋅(1-d(τ̂))の項は、計算において実際の治療Wが最適な治療方針dに対応する個人のみを使用することを意味しています。

def gain_policy(data, learner):    tau_hat = learner.effect(data[X])    e_hat = clone(model_e).fit(data[X], data[W]).predict_proba(data[X])[:,1]    d = tau_hat > cost    return np.sum((d * data[W] * (data[Y] - cost)/ e_hat + (1-d) * (1-data[W]) * data[Y] / (1-e_hat)))results = compare_methods(learners, names, gain_policy, title='経験的方策利得', subtitle='より高いほど良い')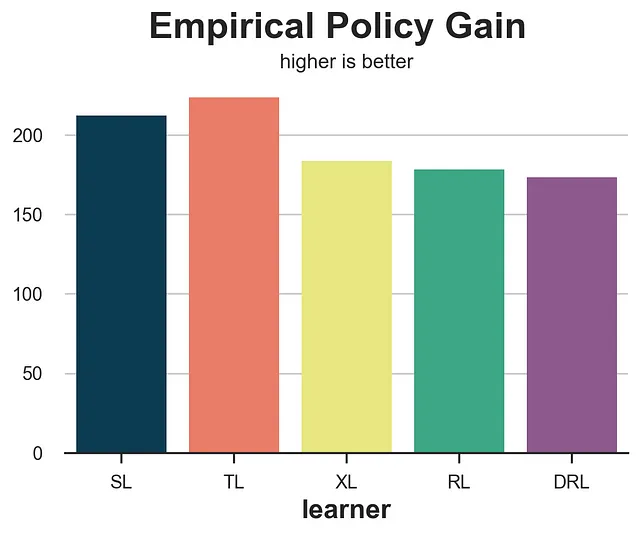

経験的方策利得は非常に優れたパフォーマンスを発揮し、S-learnerとT-learnerの2つの最も性能の悪いメソッドを分離します。

メタスタディ

この記事では、アップリフトモデル、つまり条件付き平均治療効果推定モデルを評価するための様々な手法を紹介しました。また、非常に特殊で限定的な例である私たちのシミュレーションデータセットでこれらの指標がどのように機能するかをテストしました。

Schuler、Baiocchi、Tibshirani、Shah（2018）は、対応する推定器のシミュレーションデータにおけるSロス、Tロス、Rロスを比較しました。彼らは、Rロスが「最も高性能なモデルの選択に最も一貫して導くバリデーションセットの指標である」と結論付けました。著者らはまた、いわゆる相性バイアスを検出しました。RロスやDRロスなどの指標は、対応する学習モデルに偏っている傾向があります。

Curth、van der Schaar（2023）は、理論的な観点からさらに広範な学習モデルを研究しました。彼らは「すべての実験条件において最も優れた選択基準は存在しない」と結論付けました。

Mahajan、Mitliagkas、Neal、Syrgkanis（2023）は、スコープの面で最も包括的な研究です。著者らは144のデータセットと415の推定器を対象に多くの指標を比較しました。彼らは「どの指標も他の指標よりも有意に優れているわけではないが、DR要素を使用する指標は常に候補の中にあるように思われる」と結論付けました。

結論

この記事では、アップリフトモデルを評価するための複数の手法を探求しました。メインの課題は、興味のある変数である個別の治療効果の観測不可能性です。そのため、異なる手法は他の変数を使用したり、プロキシの結果を使用したり、暗黙の最適方針の効果を近似したりすることでアップリフトモデルを評価しようとします。

どのメソッドを使用することをお勧めするのは難しいです。理論的または経験的な観点からも、最も優れた方法についての合意はありません。R-およびDR-要素を使用する損失関数は、一貫して優れた性能を発揮する傾向がありますが、対応する学習者に対してもバイアスがかかります。ただし、これらの指標がどのように機能するかを理解することは、特定のシナリオに応じて最も適切な決定をするために、それらのバイアスと制約を理解するのに役立ちます。

参考文献

• Curth, van der Schaar (2023), “In Search of Insights, Not Magic Bullets: Towards Demystification of the Model Selection Dilemma in Heterogeneous Treatment Effect Estimation”
• Gutierrez, Gerardy (2017), “Causal Inference and Uplift Modeling: A review of the literature”
• Hitsch, Misra, Zhang (2023), “Heterogeneous Treatment Effects and Optimal Targeting Policy Evaluation”
• Kennedy (2022), “Towards optimal doubly robust estimation of heterogeneous causal effects”
• Kunzel, Sekhon, Bickel, Yu (2017), “Meta-learners for Estimating Heterogeneous Treatment Effects using Machine Learning”
• Mahajan, Mitliagkas, Neal, Syrgkanis (2023), “Empirical Analysis of Model Selection for Heterogeneous Causal Effect Estimation”
• Nie, Wager (2017), “Quasi-Oracle Estimation of Heterogeneous Treatment Effects”
• Saito, Yasui (2020), “Counterfactual Cross-Validation: Stable Model Selection Procedure for Causal Inference Models”
• Schuler, Baiocchi, Tibshirani, Shah (2018), “A comparison of methods for model selection when estimating individual treatment effects”

関連記事

• メタラーナーの理解
• ダブルロバスト推定量であるAIPWの理解
• 因果推論モデルの理解
• 因果推論モデルからフォレストへ

コード

元のJupyter Notebookはこちらでご覧いただけます：

Blog-Posts/notebooks/evaluate_uplift.ipynb at main · matteocourthoud/Blog-Posts

VoAGIブログ記事のコードとノートブック。matteocourthoud/Blog-Postsの開発にご協力ください…

github.com

読んでいただきありがとうございます！

本当に感謝しています！ 🤗 もし記事が気に入った場合は、フォローをご検討ください。私は週に1回、因果推論とデータ分析に関連するトピックについて投稿しています。私の投稿はシンプルで正確であり、常にコード、例、シミュレーションを提供します。

また、免責事項もあります：学ぶために書いているので、ミスは当然ですが、最善を尽くしています。見つけた場合は教えていただけると幸いです。また、新しいトピックへの提案も歓迎します！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!