「仮説検定とA/Bテスト」

『仮説検定とA/Bテスト』

データが絶対的な支配を誇る時代において、ビジネスや組織はその力を利用する方法を常に探し続けています。

Amazonでおすすめされる商品やソーシャルメディアで見るコンテンツには、狂気的な方法の背後に入念な方法があります。

これらの決定の中心には何があるのでしょうか？

A/Bテストと仮説検定です。

しかし、それらは何であり、なぜデータ中心の世界で重要なのでしょうか？

一緒にそれらをすべて発見しましょう！

あなたの画面の魔法

統計分析の重要な目標の一つは、データ内のパターンを見つけ出し、それらのパターンを現実世界に適用することです。

そして、ここで機械学習が重要な役割を果たします！

機械学習は通常、データ内のパターンを見つけ出し、それらをデータセットに適用するプロセスと説明されます。この新しい能力により、世界中の多くのプロセスや意思決定が非常にデータ駆動型になりました。

Amazonを閲覧し、商品のおすすめを受けるたびや、ソーシャルメディアのフィードでターゲットに合わせたコンテンツを見るたびに、魔法は使われていません。

それは入念なデータ分析とパターン認識の結果です。

多くの要素が、購入したいと思うかもしれないかどうかを決定することができます。これには、前回の検索、ユーザーの人口統計情報、ボタンの色から一日の時間まで、さまざまな要素が含まれます。

そして、これがデータ内のパターンを分析することで見つけることができるものです。

AmazonやNetflixなどの企業は、閲覧した商品、気に入った商品、購入履歴など、ユーザーの行動パターンを分析する高度な推奨システムを構築しています。

しかし、データはしばしばノイズがあり、ランダムな変動があります。これらの企業は、彼らが見ているパターンが本物であることをどのように確保しているのでしょうか？

その答えは仮説検定にあります。

仮説検定：データ内のパターンの検証

仮説検定は、与えられた仮説が真である可能性を決定するために使用される統計的な方法です。

簡単に言えば、データ内の観察されたパターンが本物か、偶然の結果かを検証する方法です。

このプロセスには通常、以下のステップが含まれます：

#1. 仮説の開発

これには、真であると仮定される帰無仮説（観察結果が偶然の結果であるとすることが一般的）と、研究者が証明しようとする対立仮説が含まれます。

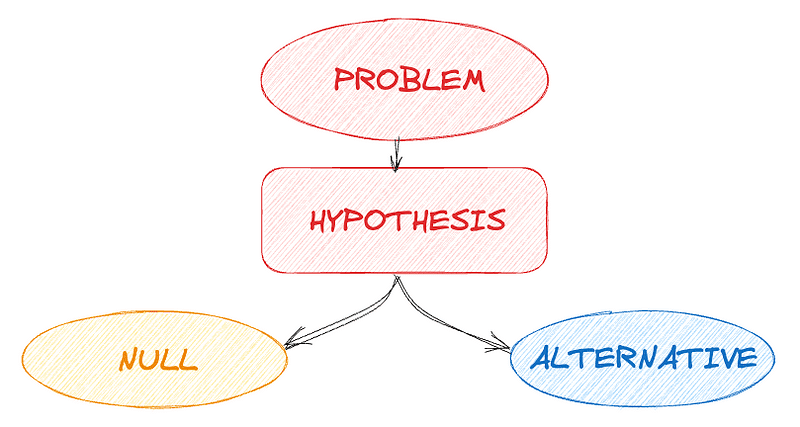
#2. テスト統計量の選択

これは、帰無仮説の真偽を判定するために使用される方法と値です。

#3. p値の計算

これは、帰無仮説が真であると仮定した場合に、観察されたテスト統計量以上に有意な統計量が得られる確率です。簡単に言えば、対応するテスト統計量の右側の確率です。

p値の主な利点は、この確率を任意の有意水準αと直接比較することで、仮説検定の最終ステップとして任意の有意水準αでテストできることです。

αは結果に置かれる信頼度を示します。つまり、αが5％の場合、信頼度は95％です。p値がα以下の場合にのみ帰無仮説が維持されます。

一般的には、p値が低いほど好ましいです。

#4. 結論の導出

p値と選択した有意水準αに基づいて、帰無仮説を受け入れるか棄却するかの判断が下されます。

例えば、企業が購入ボタンの色を変えることが売上に影響を与えるかどうかを判断したい場合、仮説検定は情報を基にした意思決定を行うための構造化された手法を提供することができます。

A/Bテスト：現実世界の応用

A/Bテストは仮説検定の実践的な応用です。これは、2つのバージョンの製品や機能を比較して、どちらがより優れているかを判断するために使用される手法です。

これには、異なるユーザーセグメントに同時に2つのバリアントを表示し、成功と追跡メトリックを使用してより成功したバリアントを決定するという手順が含まれます。

ユーザーが見るコンテンツのすべては、最大のポテンシャルを発揮するために微調整する必要があります。このようなプラットフォームでのA/Bテストのプロセスは仮説検定に類似しています。

では… ソーシャルメディアのようなもので、ユーザーが緑色のボタンを使用する場合と青色のボタンを使用する場合に、ユーザーがより関与する可能性があるかどうかを理解したいとしましょう。

それは次のようなものです：

初期調査：現在の状況を理解し、テストする必要のある機能を決定します。この場合は、ボタンの色です。
仮説の設定：これがなければ、テストキャンペーンは方向性がありません。青色を使用すると、ユーザーはより関与する可能性が高いです。
ランダムな割り当て：テスト機能のバリエーションは、ランダムにユーザーに割り当てられます。ユーザーを2つの異なるランダム化されたグループに分割します。
結果の収集と分析：テスト後、結果を収集し、分析し、成功したバリアントを展開します。

実際のA/Bテストのビジネス例

ソーシャルメディア会社であるという考えを持ちながら、実際のケースを説明してみましょう。

目標：プラットフォーム上のユーザーの関与を増やす。

測定するメトリック：プラットフォームでの平均滞在時間。これには、投稿数やいいね数などの関連するメトリックも含まれるかもしれません。

#ステップ1: 変更を特定する

ソーシャルメディア会社は、シェアボタンをより目立つように再デザインし、見つけやすくすると、より多くのユーザーが投稿を共有し、関与が増加すると仮説を立てています。

#ステップ2: 2つのバージョンを作成する

バージョンA（ヌル）：現在のプラットフォームのデザインとしてのシェアボタン。
バージョンB（代替）：同じプラットフォームですが、シェアボタンがより目立つように再デザインされています。

#ステップ3: ユーザーを分割する

会社はユーザーベースをランダムに2つのグループに分割します：

50%のユーザーはバージョンAを見ます。
50%のユーザーはバージョンBを見ます。

#ステップ4: テストを実施する

会社は30日といった一定期間テストを実施します。この間、両グループのユーザー関与メトリックのデータを収集します。

#ステップ5: 結果を分析する

テスト期間終了後、会社はデータを分析します：

バージョンBグループの平均滞在時間は増加しましたか？

#ステップ6: 決定を行う

データをすべて収集した後、2つの主要なオプションがあります：

バージョンBが関与面でバージョンAを上回った場合、会社は新しいシェアボタンデザインをすべてのユーザーに展開することを決定します。
有意な差がない場合、またはバージョンAの方が優れていた場合、会社は元のデザインを維持し、アプローチを見直すことを決定します。

#ステップ7：反復する

反復は重要であることを常に覚えておいてください！

会社はここで止まりません。彼らは他の要素をテストし、エンゲージメントを継続的に最適化することができます。

グループがランダムに選択され、彼らが経験する唯一の違いがテストされる変更であることを確認することが重要です。これにより、エンゲージメントの観察された違いが他の外部要因ではなく変更に帰因できるようになります。

推論統計：単なる違いの先へ

2つのグループのパフォーマンスを単純に比較することは簡単に思えるかもしれませんが、仮説検定などの推論統計はより構造化されたアプローチを提供します。

たとえば、新しいトレーニング方法が配達ドライバーのパフォーマンスを向上させるかどうかをテストする場合、トレーニング前と後のパフォーマンスを単純に比較するだけでは、天候条件などの外部要因により誤解を招く可能性があります。

A/Bテストを使用することで、これらの外部要因を分離して、観察された違いが治療によるものであることを確認します。

データ駆動型の世界を航海する

データに基づく意思決定がますます重要になる現代の世界では、A/Bテストや仮説検定などのツールは欠かせません。これらは科学的なアプローチを提供し、企業や組織が単なる直感ではなく経験的な証拠に頼らないようにします。

データをさらに生成し、テクノロジーが進化するにつれて、これらのツールの重要性はますます高まるでしょう。

常に覚えておいてください、データの広大な海では、情報を収集するだけでなく、それを扱い、利用する方法を学ぶことも重要です。

そして、仮説検定とA/Bテストによって、これらの課題に効果的に対処するための指針を手に入れます。

データ駆動型の決定の魅力的な世界へようこそ！ Josep Ferrerはバルセロナ出身の解析エンジニアです。彼は物理工学を卒業し、人間の移動に応用されたデータサイエンスの分野で現在働いています。彼はデータサイエンスとテクノロジーに焦点を当てたパートタイムのコンテンツクリエイターです。LinkedIn、Twitter、またはVoAGIで彼に連絡することができます。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!

Data science

Was this article helpful?

93 out of 132 found this helpful