「貪欲であることはどれほど悪いのか?」
「貪欲であることはどれほど悪いのか?」
貪欲な解法による在庫切断問題の探索
目次
- 在庫切断問題の動機
- NP困難問題の概要
- 在庫切断問題をPythonでエンコードする
- 貪欲アルゴリズム
- 低次元空間における網羅的な探索との比較
- 高次元空間におけるランダム探索との比較
- 結論
在庫切断問題の動機
私はデータサイエンティストです。データサイエンスのスキルは仕事で非常に重要ですが、データサイエンスの概念は仕事以外の多くの問題の解決にも役立つことがわかります!
私のデータサイエンスのスキルが役立つ一つの方法は、DIYや製作の趣味での活用です。切断する素材の計画を立てることは一般的な課題です。私は店から同じサイズの複数の素材を使って切断する必要があるカットのリストを持っています。できるだけ無駄を出さずにカットを計画するにはどうすればいいのでしょうか?この課題は「在庫切断問題」として知られており、実際には非常に困難な問題です(実際にはNP困難です!)
- 「マスタリングモンテカルロ:より良い機械学習モデルをシミュレーションする方法」
- データモデリング入門、パート1:データモデリングとは何ですか?
- VoAGIニュース、8月2日:ChatGPTコードインタプリタ:高速データサイエンス•追いつけない?AIの今週の話題をキャッチアップしましょう
この記事では、この問題を解決するための「近道」(言葉遊びが含まれています)を探求し、この方法が従来の方法と比較してどのようになるかを分析します。

NP困難問題の概要
ここではNP困難問題について詳しくは説明しませんが、直感的な理解を提供したいと思います。最適化問題が困難になるのは、通常、解の空間の大きさです。つまり、最適解を見つけるためにどれだけの可能な解を探索する必要があるかです。問題の難しさは、問題のサイズが大きくなるにつれて解の空間がどれだけ速く成長するかで通常評価されます。
「在庫切断問題」では、カットの数を増やすと問題が非常に大きくなります。以下に、解の空間がどれだけ速く成長するかを示します!
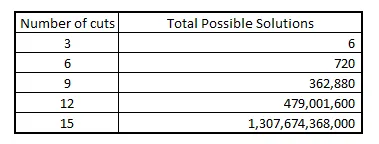
解の空間は階乗的に成長します。つまり、最適な答えを得るために検索する必要のある総解の数はn!です。これは非常に大きくなります。
NPは「非決定的多項式」を意味し、問題が多項式関数よりも速く成長することを示します。NP/NP困難問題について詳しく調べるための多くのリソースがあります。ここではこれ以上の説明はしません。
在庫切断問題をPythonでエンコードする
在庫切断問題は基本的に順序問題です。特定の順序でカットを行い、在庫の長さがなくなったら(順序通りに)次の在庫でカットを開始します。
- 視覚化がこれを最もよく説明します。例えば、以下のカットの順序があるとしましょう
- [4′, 2′, 1′, 2′, 2′, 1′] と、在庫サイズは5’です。無駄の計算は以下のようになります:
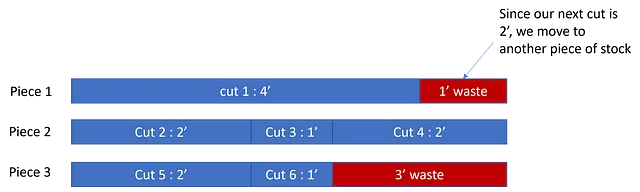
ここでは、合計の無駄は4’です。
しかし、同じカットを保持しながら順序を変更すると、異なる量の無駄が生じます。例えば、[4′, 1′, 2′, 2′, 1′, 2′] を試してみましょう:
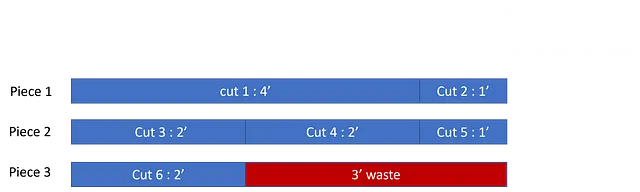
ここでは、わずか3’の廃棄物しか得られません – 単純に順序を変更するだけで廃棄物を減らすことができました!これがこの最適化問題の基本的な考え方です。どの切り方が最も良いかを見つけたいのです。
さて、これをPythonスクリプトにエンコードするために、(1) 各順序の廃棄物を計算するための関数と、(2) リストを最適な順序に並べ替えるアルゴリズムが必要です。
廃棄物を計算するための関数は、上記で概説したロジックを単純に再現するだけです。以下にPythonコードを示します:
def total_waste(stock_size, solution): ''' 特定の解に対するカットオフの廃棄物を計算する 入力 stock_size (float) : 購入可能なストックの寸法 solution (list) : カットの順序を示す浮動小数点数のリスト 出力 cut_off_waste (float) : 与えられた解のカットオフの総廃棄物 ''' # 現在のストックのカットの総長さを追跡するための変数を設定 temp_cut_length = 0 # 廃棄物なしで開始 cut_off_waste = 0 for cut in solution: # 次のカットが現在のストックに収まらない場合、 # 新しい廃棄物を計算し、別のストックのためにリセットする if temp_cut_length + cut > stock_size: # カットオフの廃棄物を計算する cut_off_waste += stock_size - temp_cut_length # カットの長さをリセットする temp_cut_length = cut else: # ストックのカットの累積長さに追加する temp_cut_length += cut # 最後のカットの廃棄物を追加する -- ループでは捕捉されない cut_off_waste += stock_size - temp_cut_length return cut_off_waste次のセクションで必要なアルゴリズムについて説明します。
貪欲アルゴリズム
貪欲アルゴリズムは非常にシンプルで、現在作業しているストックの残りに収まる最も大きなピースを見つけるだけです。
前の例を使って、これらのカット [4′, 2′, 1′, 2′, 2′, 1′] を行いたいとします。そして、順序を最適化するための貪欲アルゴリズムが必要です。
最初に、現在のストックの最も長いカットから始めます。まだカットを行っていないので、現在のストックのピースは5’です。最も長いカットは4’で、残りのストックの5’に収まります。次に長いカットは2’ですが、残りのストックが1’しかないため、長すぎます。次に長いカットは1’です。これは残りのストックに収まるので、次のカットは1’です。このアルゴリズムは、カットが残っていないまでこのパターンに従います。
Pythonでのアルゴリズムは以下のようになります:
def greedy_search(cuts, stock_size): ''' 貪欲最適解を計算する 入力: cuts (list) : 行う必要のあるカット stock_size (float) : 購入可能なストックのサイズ 出力: cut_plan (list) : 貪欲最適結果を得るためのカットの順序のシーケンス waste (float) : ソリューションによって浪費される材料の量 ''' # カットオフ計画を空にして、後で入れる cut_plan = [] # カットオフサイズをストックサイズと同じに設定 cut_off = stock_size # 元のリストを変更しないために、cutsリストをコピー cuts_copy = copy(cuts) # カットを降順でソート cuts = list(np.sort(cuts)[::-1]) # すべてのカットが順序付けられるまで # カットを順序付けることを続ける while len(cuts_copy) > 0: for cut_size in cuts_copy: # カットサイズが残りのストックより小さい場合、 # 今すぐカットを割り当てる if cut_size < cut_off: # カットを計画に追加 cut_plan.append(cut_size) # 残りの量を更新 cut_off -= cut_size # 順序付ける必要のあるカットのリストから # カットを削除 cuts_copy.remove(cut_size) # cut_offを完全なストックサイズにリセット cut_off = stock_size # total_waste関数を使用して廃棄物を計算する waste = total_waste(stock_size, cut_plan) return cut_plan, waste低次元空間での徹底的な探索との比較
貪欲アルゴリズムを使用することで、最適解の近似を得るために時間を大幅に節約していますが、その近似はどの程度良いでしょうか?解空間の徹底的な探索は、グローバル最適解を与えます – これが私たちの基準です。わずかなカットのシナリオで貪欲アルゴリズムの解をグローバル最適解と比較してみましょう(多くのカットを含む場合、グローバル最適解を見つけるのは非常に困難です)。
私は2〜10の切断サイズに合わせて250の切断リストをランダムに作成しました。各切断は0から1の間で、在庫サイズは1.1に設定されています。以下はそのパフォーマンスです:
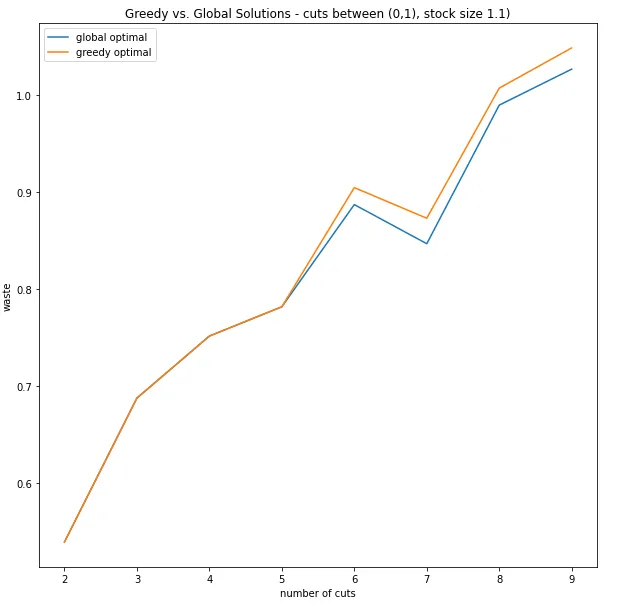
ご覧のように、’n’が増えるにつれて、貪欲なパフォーマンスはグローバルオプティマムに対して悪くなりますが、比較的近くに留まり、高い相関関係があります。
高次元空間でのランダムサーチとの比較
残念ながら、私たちは重要な盲点を持っています…つまり、高次元空間でのグローバルオプティマムを知りません。今、私たちは異なる種類のヒューリスティック(グローバルオプティマムを近似するために設計されたアルゴリズム)を比較するビジネスに入ります。貪欲アルゴリズムは、解空間のランダムサーチと比較してどのようになっていますか?
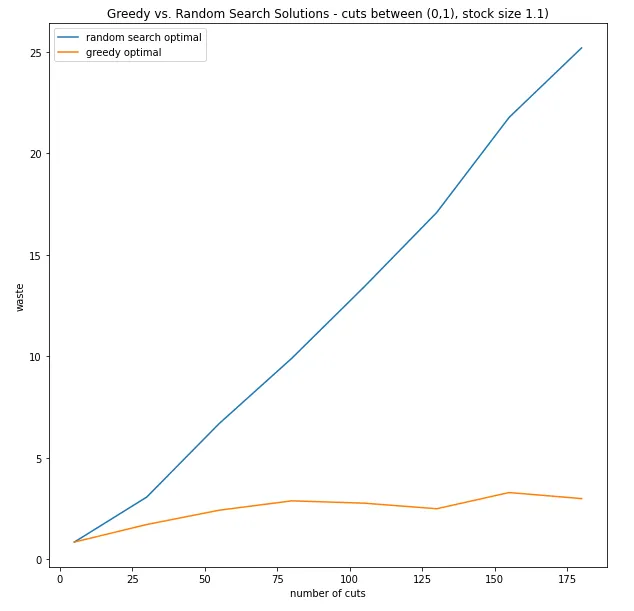
切断数が増えると、ランダムサーチは著しく悪化します。これは、ランダムサーチが500の解をランダムに選び、最良の解を選ぶためです。解空間が爆発するにつれて、私たちがランダムに探索する解空間の確率の割合はますます小さくなります。今、私たちが見ることができるのは、貪欲な解が潜在的な解をランダムに見るよりもはるかに優れているということです。
結論
在庫切断問題に対する貪欲な解は、かなり良い解を素早く見つける合理的な方法のようです。私の目的にはこれで十分です。私は年に数件のプロジェクトしか行わず、通常は小規模です。ただし、製造工場などの応用では、より複雑で集中的なアプローチが会社に大きなドルの影響を与える可能性があります。より良い最適解を探索するための別の方法として、「混合整数線形計画法」(MILP)を調べることができます。
この問題についてさらに詳しく調査する場合、貪欲アプローチをより良いメタヒューリスティックアルゴリズム(ランダムサーチはおそらく最悪のものです)と比較することができます。例えば、ヒルクライム、タブーサーチ、または焼きなまし法のさまざまなバージョンなどです。今のところここまでにしておきますが、別のテーブルを作る予定です!
この記事で使用されたすべてのコードは、このリポジトリを参照してください。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
