「ロジスティック回帰の謎解き：簡単なガイド」

Decoding the Mystery of Logistic Regression A Simple Guide

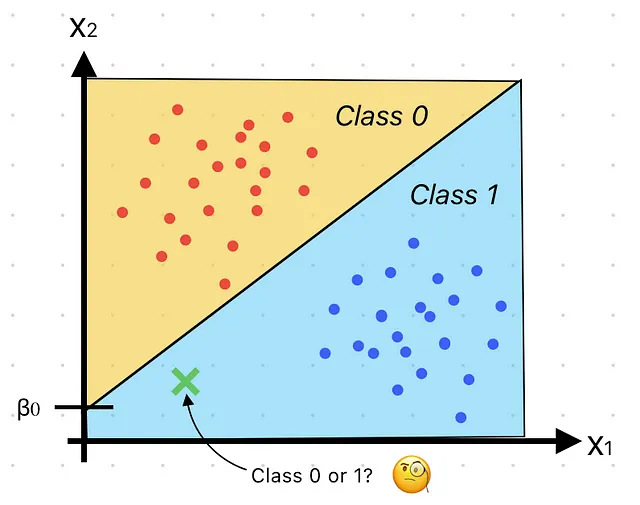
はじめに

データサイエンスと機械学習の世界では、ロジスティック回帰は強力で広く使用されるアルゴリズムです。その名前からは、物流や貨物の取り扱いに関係があるように思えますが、実際にはそれとは関係ありません。代わりに、ロジスティック回帰は分類タスクのための基本的なツールであり、何かが2つのカテゴリのうちの1つに属するかどうか、例えばはい/いいえ、真/偽、スパム/非スパムなどを予測するのに役立ちます。このブログでは、ロジスティック回帰の概念を分解し、できるだけ簡単に説明します。

ロジスティック回帰とは何ですか？

ロジスティック回帰は、教師あり学習アルゴリズムの一種です。”回帰”という用語は誤解を招くかもしれませんが、これは線形回帰のように連続値を予測するために使用されるものではありません。代わりに、バイナリ分類問題に取り組みます。つまり、単純な「はい」または「いいえ」という質問に答えることです。

大学の入学担当者であると想像してください。テストの成績に基づいて学生が入学するかどうかを予測したいとします。ロジスティック回帰は、その予測をサポートするのに役立ちます！

• 「なぜより多くがより良いのか（人工知能において）」
• ビジュアルトランスフォーマー（ViT）モデルのコードに深く潜る
• 「スロットを使用すべきですか？スロットがクラスに与える影響、それらを使用するタイミングと方法」

シグモイド関数

ロジスティック回帰の核心にあるのは、シグモイド関数です。複雑なように聞こえるかもしれませんが、これは任意の入力を0から1の値に圧縮する数学関数です。

シグモイド関数の式は次の通りです：

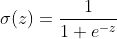
ここで：

• z は関数への入力です。

それを可視化してみましょう：

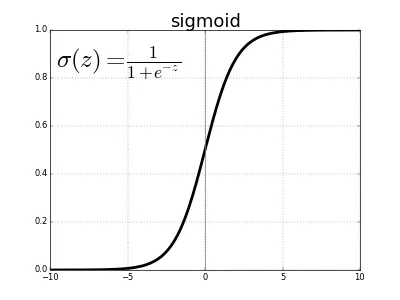
お分かりいただけるように、シグモイド関数は z が大きな正の値の場合は1に近づき、大きな負の値の場合は0に近づきます。z = 0 のとき、sigmoid(z) はちょうど0.5です。

予測の行い方

さて、シグモイド関数を理解しましたが、それが予測にどのように役立つのでしょうか？

ロジスティック回帰では、各データポイントにスコアを割り当てます。このスコアは、入力特徴量の線形組み合わせの結果です。次に、このスコアをシグモイド関数に通して、0から1の間の確率値を得ます。

数学的には、スコア z は次のように計算されます：

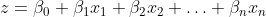
ここで：

• β（β_0、β_1、β_2、…、β_n）はアルゴリズムがトレーニングデータから学習する係数（重み）です。
• β_0はバイアス重みとしてよく知られています。
• X（x_1、x_2、…、x_n）はデータポイントの入力特徴量です。

確率 sigmoid(z) を得たら、それをデータポイントが正のクラス（例：入学）に属する可能性として解釈することができます。

閾値の設定

ロジスティック回帰は確率を提供するため、その確率に基づいて判断する必要があります。通常、0.5を閾値として設定します。sigmoid(z) が0.5以上であれば、正のクラスを予測します。そうでなければ、負のクラスを予測します。

結論

要約すると、ロジスティック回帰はバイナリ分類問題に対するシンプルで効果的なアルゴリズムです。シグモイド関数を使用してスコアを確率にマッピングするため、結果を解釈するのは容易です。

覚えておいてください、ロジスティック回帰は機械学習の広大でエキサイティングな分野の一部ですが、データサイエンスの旅における重要な基礎となります。分類を楽しんでください！

要約: ロジスティック回帰の主要なポイント：

1. 2値分類のためのロジスティック回帰：ロジスティック回帰は、2値分類タスクに使用される強力なアルゴリズムです。2つのカテゴリのどちらかに所属するかを予測し、yes/no、true/false、spam/not spamのようなシナリオに理想的です。

2. シグモイド関数：ロジスティック回帰の中核には、入力値を0から1の確率にマッピングするシグモイド関数があります。この関数は、入力特徴の線形結合を確率スコアに変換するために重要です。

3. 確率の解釈：他の回帰手法とは異なり、ロジスティック回帰は連続値の代わりに確率を生成します。これらの確率は、データポイントが陽性クラスに所属する可能性を表し、モデルの予測を明確に理解することができます。

4. 閾値の設定：実際の予測を行うためには、しきい値が設定されます（通常は0.5）。予測された確率がしきい値以上であれば、陽性クラスが予測されます。しきい値を調整することで、モデルの精度と再現率のトレードオフに影響を与えることができます。

5. 基礎となる構築要素：ロジスティック回帰は機械学習の世界で基礎的な概念であり、より複雑なアルゴリズムの基礎となります。ロジスティック回帰の理解は、より高度な分類問題の解決と、さまざまなデータサイエンスの応用領域の探索に向けた土台となります。

これらの要点を押さえることで、ロジスティック回帰が2値分類タスクの解決におけるシンプルさと重要性を理解し、機械学習の魅力的な分野をさらに探求する旅に出ることができます。

お読みいただき、ありがとうございます。ご意見やフィードバックは大変ありがたいです。

私の名前はWeiQin Chuah（同僚のほとんどはWeiと呼んでいます）で、オーストラリア・メルボルンのRMIT大学の研究フェローです。私の研究は、コンピュータビジョンの問題を解決するための堅牢な深層学習モデルの開発に焦点を当てています。LinkedInのページで私についてもっと詳しく知ることができます。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!